MOOC-athon: Week 1 of Social Network Analysis

Jumping In to MOOC Madness
I've enrolled in a MOOC. They are all the rage these days. I'm learning about Social Network Analysis courtesy of Coursera.  My friend and colleague Steve took World Music from the same outfit, and I enjoyed reading his blogs and commentary about the experience. I'm inspired to blog a bit myself about my SNA. And while this is my space to talk about marathons and bike rides and stuff, well I'm kind of taking on this MOOC in the same general spirit.

Steve had a less than thrilling experience in his course, or at least that's how I read his account of it. I'm hoping that my experience is a bit better overall. I am optimistic about this for two reasons:

1. 1. I think the topic of my course - social network analysis - lends itself a bit better to an online course at a large (huge!) scale because some of the work can be evaluated by machine. Graphs are mathematical constructs, after all, and so even when we do projects working with data sets, there can be automated responses to things. 
2. SNA is a topic I've read about, and I've even experimented with a bit, but which I don't have adequate command over to actually use in my own work as a researcher. But I think it can be very useful to me. I read most of the textbook already. So I'm motivated to learn enough to make SNA techniques useful. This is not to say that Steve wasn't motivated, but writing essays about Cuban Jazz Fusion still likely falls into the category of things he did less for professional than for personal/curiosity reasons.

Week 1: Introduction, Videos, & a (gulp) My First Graded Homework Assignment

We had four short video clips to watch this week that took me about an hour to go through. The videos had some quiz questions built in at various points to allow us to test our understand of concepts. From what I could tell, attempting the quiz is what mattered, as my syllabus status view seems to indicate.

We were also asked to download a piece of software for doing Social Network Analysis called Gephi.  I previously experimented with a much simpler program called GraphViz that uses a markup language (.dot) to create graphs. I was happy to see Gephi handles those too.

Our first homework assignment was to analyze our own Facebook social graph and to answer a few questions about the properties of our network. My sociogram appears above. In case you are wondering, there are 687 nodes (friends) and just under 14,000 edges (connections) linking them. But the big news here is that my "giant component" is nearly as large as my whole network: 675/687. What does that mean? Simply that most of my facebook friends are connected with each other. And I can also tell you that most of them are Higher Ed. colleagues. That's the big blue mass up there.

How the assignment worked 
We were to use a simple .txt file to record answers to questions about our network's features. These questions corresponded to the concepts in lecture 1C. Then, we had to upload the answers and our graph file to an automated script that ran the same analyses we were supposed to do, compared the numbers we listed as answers to the questions, and then assigned a score.


I was a bit nervous waiting for the response to come back. I was about 66% confident I'd done it correctly. I guess I did.

Pedagogical Tips
I didn't have a lot of trouble getting this first bit of work done, but I did struggle just a bit to connect the conceptual material with the procedural steps for doing both the quizzes embedded in the lecture and the assignment. What I mean is that each time, there were key procedural steps that I was focusing on getting right that seemed only loosely connected to the more interesting concepts we were asked to consider in the lecture.

My advice to my instructor would be to clarify as much of the procedural stuff as possible - something that might require going back through the discussion forums and revising lecture slides and/or assignment sheets.

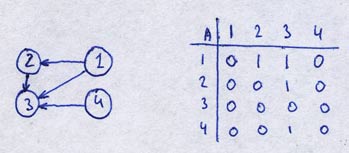
Here's one example: performing simple computations on a graph using adjacency matrices. One key fact was left out of the example and the explanation, it seems to me: the X axis refers to the source node and the Y axis refers to target nodes. Knowing this helps to clarify which dimension refers to inbound or outbound links.

That's not that important of a thing, really, conceptually. But it is a dealbreaker procedurally if you are trying to get the right answer to a quiz question in which you have a graph like the one on the left and you have to identify the matrix that represents it.

Anyway...so far so good. The instructors could sweat the details a bit more, but we will see how things progress. I'm having fun so far!